Home › Dark Side Of Pop Culture

The Intricate World Of The Sine Graph: Discovering Its Applications And Properties

williamfaulkner November 25, 2024

The Intricate World Of The Sine Graph: Discovering Its Applications And Properties

Have you ever wondered how the sine graph, a fundamental concept in trigonometry, plays a crucial role in various fields such as physics, engineering, and even music? The sine graph is more than just a wavy line on a graph; it's a mathematical function that helps us understand periodic phenomena. Whether you're a student trying to grasp its concepts or a professional looking to apply it in a real-world context, understanding the sine graph is essential. Its unique properties make it a vital tool in analyzing waves, oscillations, and other repetitive patterns.

The sine graph is a visual representation of the sine function, which is one of the three primary trigonometric functions. It is characterized by its smooth, continuous wave-like pattern, which repeats every 360 degrees or 2π radians. The graph's shape and properties are influenced by its amplitude, period, phase shift, and vertical shift. These elements allow the sine graph to model various cyclical behaviors, making it indispensable in sciences and mathematics.

Understanding the sine graph is not only about learning its mathematical properties but also about exploring its practical applications. From signal processing to electrical engineering, the sine graph helps us model and analyze phenomena that exhibit periodic behavior. Its applications extend to diverse areas, including sound waves, light waves, and even the stock market. This article delves into the sine graph's intricacies, exploring its mathematical framework, historical significance, and real-world applications, providing a comprehensive guide for students, educators, and professionals alike.

Table of Contents

The Mathematical Foundation of the Sine Graph
- The Sine Function: A Trigonometric Perspective
- Understanding the Unit Circle
Key Properties of the Sine Graph
- Amplitude and its Influence
- Period of the Sine Graph
- Phase Shift: Analyzing Horizontal Translations
- Vertical Shift: Adjusting the Baseline
Graphing the Sine Function: Step-by-Step Guide
- Plotting Basic Sine Graphs
- Transformations of the Sine Graph
Applications of the Sine Graph in Real Life
- Physics and Engineering Applications
- Understanding Sound Waves and Music
- Sine Graphs in Electrical Engineering
Advanced Concepts: Fourier Series and Sine Waves
- Introduction to Fourier Series
- Sine Waves in Signal Processing
The Historical Development of the Sine Graph
- Origins and Evolution
- Pioneers in Trigonometry
Common Mistakes and Misconceptions
- Avoiding Graphing Errors
- Understanding Negative Values
FAQs
Conclusion

The Mathematical Foundation of the Sine Graph

The sine graph is rooted in the fundamental principles of trigonometry. To comprehend its intricacies, one must first understand the sine function, a cornerstone of trigonometric concepts. The sine function is defined for all real numbers and is periodic, with a period of 2π radians. This periodic nature is what gives the sine graph its characteristic wave-like appearance.

The Sine Function: A Trigonometric Perspective

Trigonometry is the branch of mathematics that deals with the relationships between the angles and sides of triangles. The sine function is one of the primary trigonometric functions, along with cosine and tangent. It is defined as the ratio of the length of the opposite side to the hypotenuse in a right-angled triangle. Mathematically, it is expressed as sin(θ) = opposite/hypotenuse.

In the context of the unit circle, which is a circle with a radius of one centered at the origin of a coordinate plane, the sine of an angle θ is the y-coordinate of the point where the terminal side of the angle intersects the circle. This geometric interpretation is fundamental to understanding how the sine graph is derived from the sine function.

Understanding the Unit Circle

The unit circle is a powerful tool in trigonometry, providing a geometric representation of the sine function. By examining the unit circle, one can visualize how the sine function varies as the angle θ changes. As the angle increases from 0 to 2π radians, the y-coordinate of the intersection point traces the sine graph's familiar wave pattern.

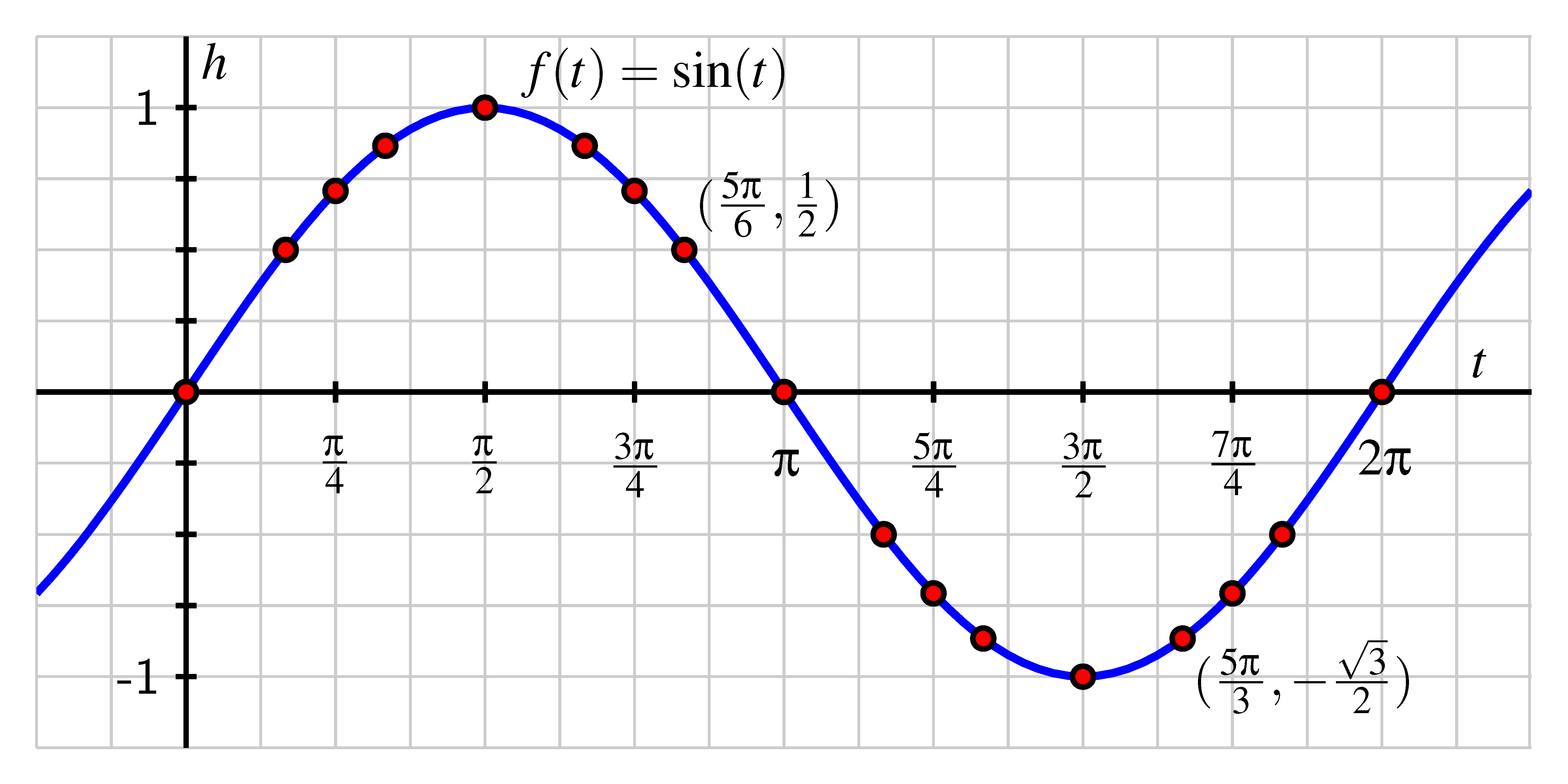
Key points on the unit circle, such as 0, π/2, π, 3π/2, and 2π, correspond to important points on the sine graph, including its maximum, minimum, and zero crossings. Understanding these points and their corresponding values helps in sketching and analyzing the sine graph.

Key Properties of the Sine Graph

The sine graph is characterized by several key properties that define its shape and behavior. These properties include amplitude, period, phase shift, and vertical shift. Each of these elements can be adjusted to transform the sine graph, making it a versatile tool for modeling various real-world phenomena.

Amplitude and Its Influence

The amplitude of a sine graph represents the maximum deviation of the graph from its central axis. It is a measure of how "tall" the waves of the graph are. In the function y = A sin(θ), the amplitude is denoted by the absolute value of A. A larger amplitude results in taller waves, while a smaller amplitude results in shorter waves.

The amplitude is significant in applications where the magnitude of oscillations is crucial, such as in sound waves, where it corresponds to loudness, and in electrical signals, where it affects signal strength.

Period of the Sine Graph

The period of a sine graph is the length of one complete cycle of the wave. For the basic sine function y = sin(θ), the period is 2π radians. This means the function repeats its pattern every 2π radians. The period can be altered by introducing a frequency factor, ω, in the function y = sin(ωθ), which changes the period to 2π/ω radians.

Understanding the period is essential for analyzing phenomena that repeat over time, such as seasonal changes, pendulum swings, and alternating current in electrical circuits.

Phase Shift: Analyzing Horizontal Translations

Phase shift refers to the horizontal translation of the sine graph along the x-axis. It is determined by the phase constant, φ, in the function y = sin(θ + φ). A positive phase shift moves the graph to the left, while a negative phase shift moves it to the right.

Phase shifts are important in synchronizing signals in telecommunications and aligning waves in physics experiments. They allow the sine graph to match the phase of real-world waveforms for accurate modeling.

Vertical Shift: Adjusting the Baseline

The vertical shift of a sine graph is the upward or downward translation along the y-axis. It is determined by the constant term, C, in the function y = A sin(θ) + C. A positive vertical shift raises the entire graph, while a negative vertical shift lowers it.

Vertical shifts are used to adjust the baseline of the sine graph in applications where the average value needs to be altered, such as in offsetting signals in electronics or adjusting the mean sea level in tidal analyses.

Graphing the Sine Function: Step-by-Step Guide

Graphing the sine function involves plotting its values over a range of angles and observing the resulting wave pattern. This process can be broken down into several steps, allowing for a systematic approach to sketching both basic and transformed sine graphs.

Plotting Basic Sine Graphs

The basic sine graph, y = sin(θ), is plotted by calculating the sine values for angles typically ranging from 0 to 2π radians. Key angles such as 0, π/2, π, 3π/2, and 2π are used to mark important points on the graph, including the maximum, minimum, and zero crossings.

Once these points are plotted, the wave-like pattern of the sine graph emerges, characterized by its smooth, continuous nature. The graph's symmetry and periodicity make it easy to extend beyond the initial cycle, repeating the pattern indefinitely.

Transformations of the Sine Graph

Transformations of the sine graph involve modifying its properties such as amplitude, period, phase shift, and vertical shift. Each transformation alters the graph's appearance, allowing it to model different real-world phenomena.

For example, increasing the amplitude results in taller waves, altering the period changes the frequency of oscillations, adjusting the phase shift moves the graph horizontally, and changing the vertical shift raises or lowers the entire graph. By combining these transformations, the sine graph can be tailored to fit specific applications and requirements.

Applications of the Sine Graph in Real Life

The sine graph is not limited to theoretical mathematics; it has a wide range of practical applications in various fields. Its ability to model periodic behavior makes it invaluable in physics, engineering, music, and more.

Physics and Engineering Applications

In physics, the sine graph is used to represent wave phenomena such as light waves, sound waves, and water waves. Its periodic nature allows it to model oscillatory motion, such as the swinging of a pendulum or the vibrations of a tuning fork.

In engineering, the sine graph is employed in signal processing, where it helps analyze alternating current (AC) signals, modulate radio waves, and design filters. Its predictable pattern makes it ideal for modeling repetitive processes and understanding resonance in mechanical systems.

Understanding Sound Waves and Music

Sound waves are a prime example of how the sine graph is applied in real life. The graph's amplitude corresponds to the loudness of the sound, while its frequency relates to the pitch. Musicians and audio engineers use the sine graph to visualize sound waves, design synthesizers, and create music with precise tonal qualities.

In the realm of acoustics, the sine graph helps analyze the harmonic content of sounds, allowing the identification of fundamental frequencies and overtones. This analysis is crucial for tuning musical instruments and optimizing sound quality in recording studios.

Sine Graphs in Electrical Engineering

Electrical engineers rely on the sine graph to understand AC signals, which are the backbone of power distribution systems. The graph's periodic nature reflects the alternating flow of current, enabling engineers to design transformers, rectifiers, and other components that rely on sinusoidal waveforms.

Furthermore, the sine graph is used in the analysis and design of communication systems, where it aids in modulating signals for transmission and demodulating them at the receiver end. Its ability to represent phase, frequency, and amplitude makes it a versatile tool in the field of electronics.

Advanced Concepts: Fourier Series and Sine Waves

The sine graph is a fundamental component of more advanced mathematical concepts, such as Fourier series and signal processing. These concepts build upon the sine graph to analyze complex waveforms and signals.

Introduction to Fourier Series

Fourier series is a mathematical technique used to decompose complex periodic functions into simpler sine and cosine components. It allows the representation of any periodic function as a sum of sine and cosine functions, each with its own amplitude and frequency.

This decomposition is instrumental in signal processing, where it helps analyze and synthesize signals with multiple frequencies. By understanding the Fourier series, engineers and scientists can break down intricate waveforms into their constituent sine waves for further analysis and manipulation.

Sine Waves in Signal Processing

Signal processing is a field that heavily relies on the sine graph to analyze, filter, and manipulate signals. The sine graph's ability to represent periodic behavior makes it a key tool in designing filters that isolate specific frequencies, removing noise, and enhancing signal quality.

In digital signal processing, sine waves are used to test and calibrate systems, ensuring accurate performance and reliable communication. The sine graph's mathematical properties enable precise control over signal characteristics, making it essential in modern technology.

The Historical Development of the Sine Graph

The sine graph has a rich history, tracing back to ancient civilizations and evolving through the contributions of mathematicians over the centuries. Understanding its historical development provides insight into its significance in mathematics and science.

Origins and Evolution

The concept of the sine function dates back to ancient India, where it was used in astronomy and geometry. Indian mathematicians such as Aryabhata and Bhaskara made significant contributions to its development, laying the groundwork for its use in trigonometry.

In the medieval Islamic world, mathematicians like Al-Khwarizmi and Al-Battani expanded upon these ideas, introducing the sine function to the Western world. Their work paved the way for the formalization of trigonometry in Europe during the Renaissance.

Pioneers in Trigonometry

The modern understanding of the sine graph is attributed to European mathematicians like Johannes Kepler, who used it to describe planetary motion, and Leonhard Euler, who formalized its mathematical properties in the 18th century.

These pioneers laid the foundation for the widespread use of the sine graph in mathematics, physics, and engineering. Their contributions have made the sine graph an indispensable tool in scientific research and technological advancements.

Common Mistakes and Misconceptions

Despite its widespread use, the sine graph is often misunderstood or misrepresented. Common mistakes and misconceptions can lead to errors in graphing and interpretation, hindering its effective application.

Avoiding Graphing Errors

One common mistake is incorrectly plotting the sine graph's key points, leading to an inaccurate representation of its wave pattern. Ensuring that key angles and their corresponding values are accurately plotted is essential for a correct graph.

Another error is neglecting to account for transformations such as amplitude changes, phase shifts, and vertical shifts. These transformations alter the graph's appearance, and failing to apply them correctly can result in misinterpretation.

Understanding Negative Values

Misunderstanding the role of negative values in the sine graph can lead to incorrect conclusions. The sine function can take negative values, representing the graph's descent below its central axis. Recognizing this behavior is important for accurate analysis and modeling.

Additionally, negative phase shifts and vertical shifts require careful consideration, as they affect the graph's orientation and baseline. Understanding these negative transformations ensures a comprehensive understanding of the sine graph's properties.

FAQs

What is a sine graph and what does it represent?
The sine graph is a visual representation of the sine function, a periodic mathematical function used to model wave-like patterns and oscillations. It is characterized by a smooth, continuous wave pattern that repeats every 2π radians.
How do amplitude and period affect the sine graph?
The amplitude determines the height of the waves on the sine graph, while the period dictates the length of one complete cycle. Changing these parameters alters the graph's appearance, making it suitable for modeling different phenomena.
How is the sine graph used in real-world applications?
The sine graph is used in various fields such as physics, engineering, and music to model periodic behavior, analyze waveforms, and design systems that rely on oscillatory motion.
What is the significance of phase shift and vertical shift in the sine graph?
Phase shift refers to the horizontal translation of the sine graph, while vertical shift represents its vertical translation. These shifts adjust the graph's alignment and baseline, allowing for precise modeling of real-world signals.
What are some common mistakes when graphing the sine function?
Common mistakes include inaccurately plotting key points, neglecting transformations, and misunderstanding negative values. Ensuring accurate representation and understanding of these elements is crucial for correct graphing.
How has the sine graph evolved throughout history?
The sine graph has evolved from ancient Indian mathematics to modern trigonometry, with contributions from Islamic and European mathematicians. Its development has made it a fundamental tool in mathematics and science.

Conclusion

The sine graph is a fundamental concept in mathematics that transcends theoretical boundaries to find practical applications in various fields. Its periodic nature and unique properties make it an invaluable tool for modeling and analyzing wave phenomena, oscillatory motion, and other repetitive patterns. By understanding the sine graph's mathematical framework, historical development, and real-world applications, one can appreciate its significance and versatility.

Through its transformations, the sine graph can be tailored to fit specific needs, making it a powerful tool in physics, engineering, music, and beyond. As we continue to explore the complexities of the sine graph, its role in advancing technology and understanding the natural world remains ever significant. Whether you're a student, educator, or professional, mastering the sine graph opens doors to a deeper comprehension of the world around us.

Article Recommendations